Автономды жүйе (математика) - Autonomous system (mathematics)
Жылы математика, an автономды жүйе немесе автономды дифференциалдық теңдеу Бұл жүйе туралы қарапайым дифференциалдық теңдеулер тәуелді емес тәуелсіз айнымалы. Айнымалы уақыт болған кезде олар да аталады уақыт өзгермейтін жүйелер.
Жылы көптеген заңдар физика, онда тәуелсіз айнымалы әдетте қабылданады уақыт, автономды жүйелер ретінде көрсетіледі, өйткені ол қабылданады табиғат заңдары қазіргі уақыттағы немесе болашақтың кез-келген нүктесімен бірдей.
Автономды жүйелер тығыз байланысты динамикалық жүйелер. Кез-келген автономды жүйені динамикалық жүйеге айналдыруға болады[дәйексөз қажет ] және өте әлсіз болжамдарды қолдана отырып[дәйексөз қажет ], динамикалық жүйені автономды жүйеге айналдыруға болады[дәйексөз қажет ].
Анықтама
Ан автономды жүйе Бұл қарапайым дифференциалдық теңдеулер жүйесі форманың
қайда х мәндерді қабылдайды n-өлшемді Евклид кеңістігі; т көбінесе уақыт деп түсіндіріледі.
Ол формадағы дифференциалдық теңдеулер жүйесінен ерекшеленеді
онда жүйенің эволюциясын реттейтін заң орын алады емес тек жүйенің ағымдағы күйіне, сонымен қатар параметріне байланысты т, қайтадан жиі уақыт ретінде түсіндіріледі; мұндай жүйелер анықтамасы бойынша автономды емес.
Қасиеттері
Келіңіздер бірегей шешімі болуы мүмкін бастапқы мән мәселесі автономды жүйе үшін
- .
Содан кейін шешеді
- .
Шынында да, белгілеу Бізде бар және , осылайша
- .
Бастапқы шарт үшін тексеру маңызды емес,
- .
Мысал
Теңдеу автономды, өйткені тәуелсіз айнымалы, оны атайық , теңдеуде анық көрінбейді. Кескінін салу көлбеу өріс және изоклин осы теңдеу үшін келесі кодты пайдалануға болады GNU октавасы /MATLAB
Ffun = @(X, Y)(2 - Y) .* Y; % функциясы f (x, y) = (2-y) y[X, Y] = мешрид(0:.2:6, - 1:.2:3); % учаске өлшемдерін таңдайдыDY = Ffun(X, Y); DX = бір(өлшемі(DY)); % сюжет мәндерін жасайдыдіріл(X, Y, DX, DY, 'k'); % бағыт өрісін қара түспен салыңызұстаңыз қосулы;контур(X, Y, DY, [0 1 2], 'g'); % жасылға изоклиндерді қосады (0 1 2)тақырып('F (x, y) = (2-y) y үшін көлбеу өріс және изоклиндер')Сюжеттен функцияны байқауға болады болып табылады -invariant, және де ерітіндінің формасы, т.а. кез-келген ауысым үшін .
Теңдеуін символдық түрде шешу MATLAB, жүгіру арқылы
ж = еріту('Dy = (2-y) * y', 'x'); % теңдеуді символикалық түрде шешедібіз екі аламыз тепе-теңдік шешімдер, және , және белгісіз тұрақтыға қатысты үшінші шешім ,
ж(3) = - 2 / (эксп(C3 - 2 * х) - 1)Үшін белгілі бір мәндерді алу бастапқы шарт, бірнеше шешімнің сюжетін қосуға болады
y1 = еріту('Dy = (2-y) * y', 'y (1) = 1', 'x'); % бастапқы мән мәселесін символикалық түрде шешедіy2 = еріту('Dy = (2-y) * y', 'y (2) = 1', 'x'); әр түрлі бастапқы шарттар үшін%y3 = еріту('Dy = (2-y) * y', 'y (3) = 1', 'x'); y4 = еріту('Dy = (2-y) * y', 'y (1) = 3', 'x');y5 = еріту('Dy = (2-y) * y', 'y (2) = 3', 'x'); y6 = еріту('Dy = (2-y) * y', 'y (3) = 3', 'x');ezplot(y1, [0 6]); ezplot(y2, [0 6]); % шешімдерді салуezplot(y3, [0 6]); ezplot(y4, [0 6]); ezplot(y5, [0 6]); ezplot(y6, [0 6]);тақырып('Көлбеу өріс, изоклиндер және f (x, y) = (2-y) y үшін шешімдер')аңыз('Көлбеу өріс', 'Isoclines', «Шешімдер y_ {1..6}»);мәтін([1 2 3], [1 1 1], strcat(' сол жақ', {'y_1', 'y_2', 'y_3'}));мәтін([1 2 3], [3 3 3], strcat(' сол жақ', {'y_4', 'y_5', 'y_6'}));тор қосулы;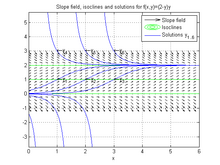
Сапалық талдау
Көмегімен автономды жүйелерді сапалы талдауға болады фазалық кеңістік; бір айнымалы жағдайда бұл фазалық сызық.
Шешу әдістері
Бір өлшемді автономды дифференциалдық теңдеулерге келесі әдістер қолданылады. Кез-келген бір өлшемді теңдеу мәніне тең -өлшемді бірінші реттік жүйе (сипатталғандай) Қарапайым дифференциалдық теңдеу # Бірінші ретті жүйеге келтіру ), бірақ керісінше емес.
Бірінші тапсырыс
Бірінші ретті автономды теңдеу
болып табылады бөлінетін, сондықтан оны ажырамас формаға келтіру арқылы оңай шешуге болады
Екінші тәртіп
Екінші ретті автономды теңдеу
қиынырақ, бірақ оны шешуге болады[1] жаңа айнымалыны енгізу арқылы
және екінші туынды туралы (арқылы тізбек ережесі ) сияқты
бастапқы теңдеу болады
бұл тәуелсіз айнымалыға сілтеме жоқ бірінші ретті теңдеу және егер шешілген болса функциясы ретінде . Содан кейін. Анықтамасын еске түсірейік :
бұл жасырын шешім.
Ерекше жағдай: х'' = f(х)
Ерекше жағдай тәуелді емес
бөлек емдеудің пайдасы.[2] Бұл теңдеулер түрлері өте кең таралған классикалық механика өйткені олар әрқашан Гамильтондық жүйелер.
Идея - жеке тұлғаны пайдалану (тыйым салу) нөлге бөлу мәселелер)
бұл тізбек ережесі. Сонымен қатар, бірінші ретті автономды жүйенің екі жағын да инверсиялау арқылы бірден қатысты интеграцияланатынын ескеріңіз :
бұл айнымалыларды бөлудің техникасын қараудың тағы бір әдісі. Сонда табиғи сұрақ туындайды: біз жоғары деңгейлі теңдеулермен осылай жасай аламыз ба? Екінші ретті теңдеулер үшін жауап иә, бірақ көп жұмыс істеу керек. Екінші туынды туынды ретінде көрсетілуі керек орнына :
Қайта атап өту керек: орындалған нәрсе - екінші туынды туынды ретінде көрсетілген . Содан кейін екінші ретті теңдеуді түпкілікті біріктіруге болады:
Бұл жасырын шешім, одан тыс үлкен проблема интегралдарды оңайлата алмау болып табылады, бұл интеграция тұрақтыларын бағалауда қиындықтар немесе мүмкін еместіктерді білдіреді.
Ерекше жағдай: х'' = х'n f(х)
Жоғарыда келтірілген менталитетті қолдана отырып, біз техниканы жалпы теңдеуге кеңейте аламыз
қайда параметрі екіге тең емес. Бұл жұмыс істейді, өйткені екінші туынды -ның дәрежесін қамтитын түрінде жазуға болады . Екінші туынды қайта жазу, қайта құру және туынды ретінде сол жағын көрсету:
Оң жақта +/- болады тең. Емдеу әр түрлі болуы керек :
Жоғары тапсырыстар
Үшінші немесе жоғары ретті автономды теңдеулерді шешудің ұқсас әдісі жоқ. Мұндай теңдеулерді, мысалы, басқа жеңілдететін қасиетке ие болған жағдайда ғана дәл шешуге болады сызықтық немесе теңдеудің оң жағының тек тәуелді айнымалыға тәуелділігі[3][4] (яғни оның туындылары емес). Үш өлшемді сызықты емес автономды жүйелер шынымен де өндіре алатындығын ескерсек, бұл таңқаларлық емес ретсіз сияқты мінез-құлық Lorenz аттракторы және Rössler аттракторы.
Бұл менталитетке сәйкес, екінші ретті жалпы автономды емес теңдеулерді нақты түрде шешуге болмайтыны таңқаларлық емес, өйткені олар хаосты да болуы мүмкін (мысалы, мезгіл-мезгіл мәжбүр болатын маятник[5]).
Сондай-ақ қараңыз
Әдебиеттер тізімі
- ^ Бойс, Уильям Э .; Ричард C. ДиПрима (2005). Бастапқы дифференциалдық теңдеулер және көлемдік есептер (8-ші басылым). Джон Вили және ұлдары. б. 133. ISBN 0-471-43338-1.
- ^ Екінші ретті автономды теңдеу кезінде eqworld.
- ^ Үшінші ретті автономды теңдеу кезінде eqworld.
- ^ Төртінші ретті автономды теңдеу кезінде eqworld.
- ^ Бланчард; Девани; Холл (2005). Дифференциалдық теңдеулер. Brooks / Cole Publishing Co., 540–543 беттер. ISBN 0-495-01265-3.



















































